動的計画法

動的計画法 (Dynamic Programming)

講義資料

資料

例題紹介

例題と課題は別々になっています。例題の方は、正解プログラム例まで紹介しますが、課題の方は、ヒント＋入出力まわりのプログラムだけ配ります。

例題ですが、ACM ICPC という国際大学対向プログラミングコンテストの2007年アジア予選東京大会の問題C (pdf) です。

プログラムおよびサンプルデータは、dp directory 以下に配置してあります。git を更新してください。

backgammon.c
サンプルデータ（入力、正解）：sample.in, sample.ans
確認用データ（入力、正解）： C.in, C.ans

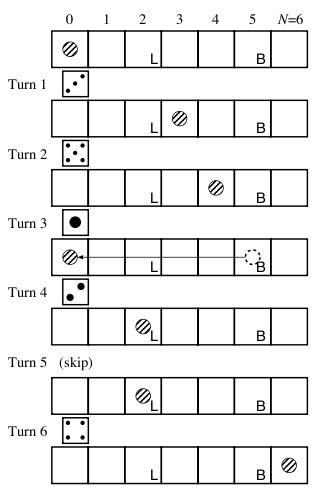
問題文が英語なので、簡単に要約すると、対象とするのはバックギャモンを単純化したゲーム。

左端からスタート、右端がゴール
- スタート:0, ゴール: N, 制約: 5 ≤ N ≤ 100
サイコロを振って、目の数だけ進む
- ゴールを超えたら、その分戻る
- L: 1回休み
- B: スタートに戻る
質問： T 回以内にゴールにたどり着く確率は？ (1 ≤ T ≤ 100)

試行錯誤

とりあえず、少し考えてみましょう。最初は、必ずスタートにいて、1/6 の確率で、位置： 1-6 に移動するわけです。但し、L についたら一回休みだし、B についたら、スタートに戻るんですが。

さて、仮に、サイコロのパターンを全部試したらどうなるでしょう？

サイコロを 10 回振ったときのパターン： 6の10乗～60Mぐらい。
サイコロを 20 回振ったときのパターン： 6の20乗～3600ペタぐらい？
サイコロ 100回なんて、気が遠くなる。。。

てな具合です。真面目にやると大変な回数ですね。まあ、サンプリングで近似的に割合を求めるって方法（モンテカルロ法）もありますが、今回は、現み使いを求めてみましょう。

組み合わせを全て求めると上記のように発散してしまうわけですが、幅優先探索の時みたいに、探索枝の合流をうまく処理すれば、無駄な計算をしなくても済む気がします。

解法

今回、f(k,p) を、k 回目のサイコロを振ったあと、位置 p に到着する確率とします。 “B” のマスに入ったときは、位置 0 に到着することにしておきます。

このとき、f(k, p) は、 f(k-1, ?) および f(k-2, ?) が分かっていれば、求められるはずです。

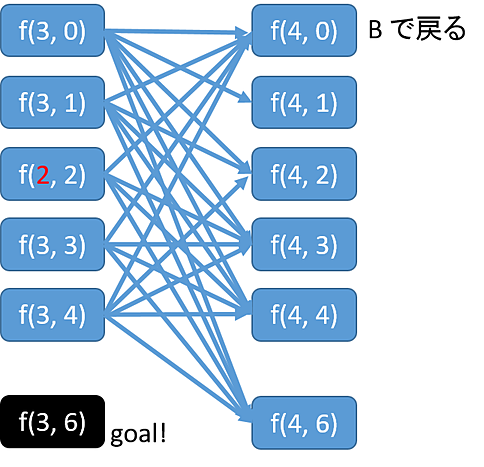
以下のプログラムは、f(k-2, ?) と f(k-1, ?) の結果を次段に反映させていれば、f(k, p)を求められるはずって感じのプログラムのイメージです。まあ、L に入ったときや、B に入ったときの処理がちょっと面倒ですけど、まあ解けそうな気がしますよね？

int solve() {
    for(/* 0 回目から t 回目まで*/) {
        for(/* 位置 0 から位置 n-1 まで*/) {
            for(/* サイコロ 1, .., 6 */) {
                int nextPos; /* 次の位置は分かる */
                int nextTurn; /* 次のターンもわかる */
                /* f(nextTurn, nextPos) を更新 */
            }
        } 
    }
}

プログラム解説

プログラムbackgammon.cの解説を簡単にしておきます。

board: 盤面情報
- board[0]: スタート, board[n]: ゴール, n 番要素までアクセスするので注意
- state_t: W(空白), L(一回休み), B(振り出しに戻る)を表す enum 型
double solve(int n, int t)
- 皆さんに実装してほしい関数
- 与えられた board の状態と、n: 盤面サイズ情報, t: ターン数に対して、解を求める。
double prob[MAX_T+2][MAX_N+1]: 解説図中の f(k, p) を格納するための配列
実際のsolve()関数の中身も、上の疑似コードとおなじですよね。